어느덧 3주차입니다. 오늘은 딥러닝 2단계 신경망과 로지스틱 회귀를 끝내 보겠습니다.
2-(4) Gradient Descent
2주차에서는 loss function을 기반으로 한 Cost Function(비용함수)에 대해 배워 봤습니다.
비용함수는 데이터 셋의 예측 정도가 얼마나 정확한지를 측정합니다.
Gradient Descent (경사하강법)은 비용함수의 오차값이 줄어들도록 파라미터 w,b를 찾는 과정을 의미합니다.
최솟값을 갖게 하는 변수의 값을 계산하는것. 대학생이라면 정말 익숙한 내용일 것입니다. 미분이죠!
Gradient Descent(경사하강법)은 미분을 통해 Cost Function(비용함수)가 가장 작은 값을 갖도록 하는 알고리즘입니다.
Cost function(비용함수)는 다음과 같았습니다.
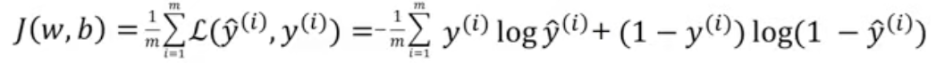
Gradient Descent는 다음과 같은 과정을 반복합니다.
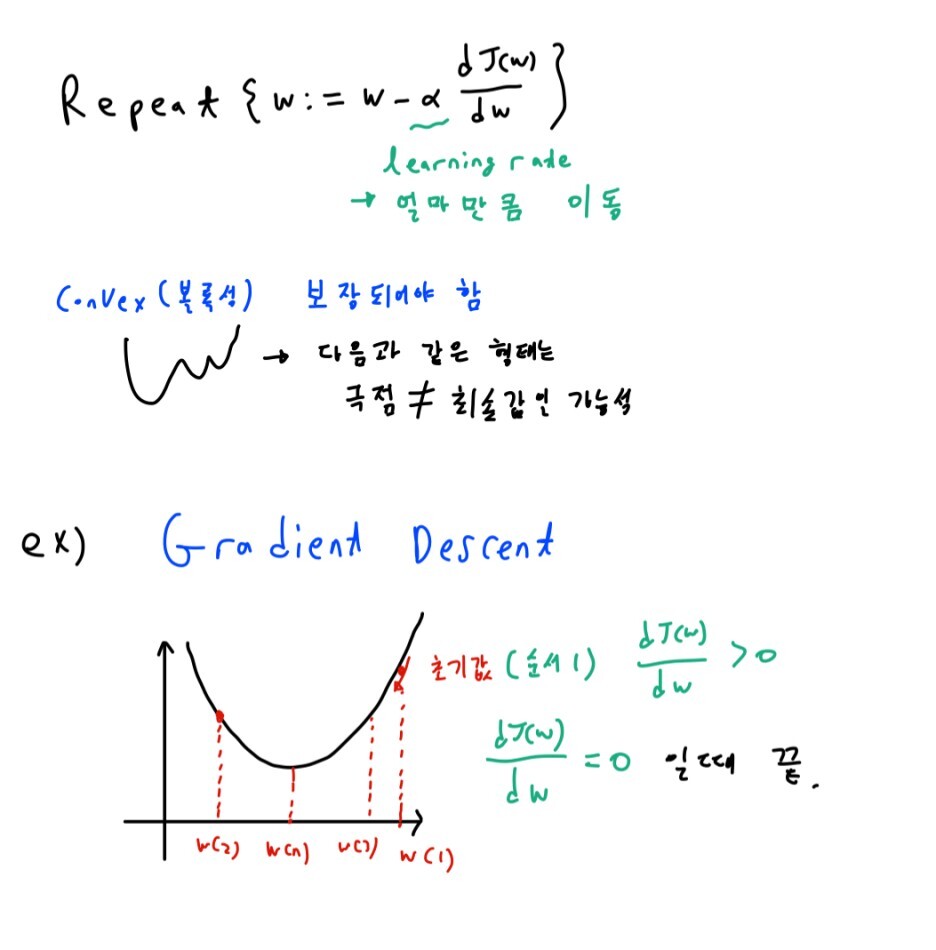
Gradient Descent(경사 하강법)에서 중요한 점은 그래프의 볼록성이 유지되어야 한다는 것입니다. cost function(비용 함수)를 위의 함수로 이용하는 것도 볼록성 때문입니다. 볼록성이 유지되지 않으면, 극점이 최솟값이지 않을 수도 있기에, cost function(비용함수)가 제일 작지 않을 수도 있습니다.
볼록성이 보장되는 식에서 Gradient Descent(경사 하강법)을 반복하면 결과적으로, 최솟값을 갖게하는 변수의 값을 찾게 됩니다.
다만 실제 cost function(비용함수)에서 최솟값을 갖는 w,b를 찾는 과정은 위의 그래프와 약간은 다릅니다. 변수의 개수가 cost function(비용함수)에서는 한 개가 더 많습니다. 그렇기에 실제 그래프는 다음과 같습니다. 변수가 하나 추가된다는 점을 제외하고는 같습니다.
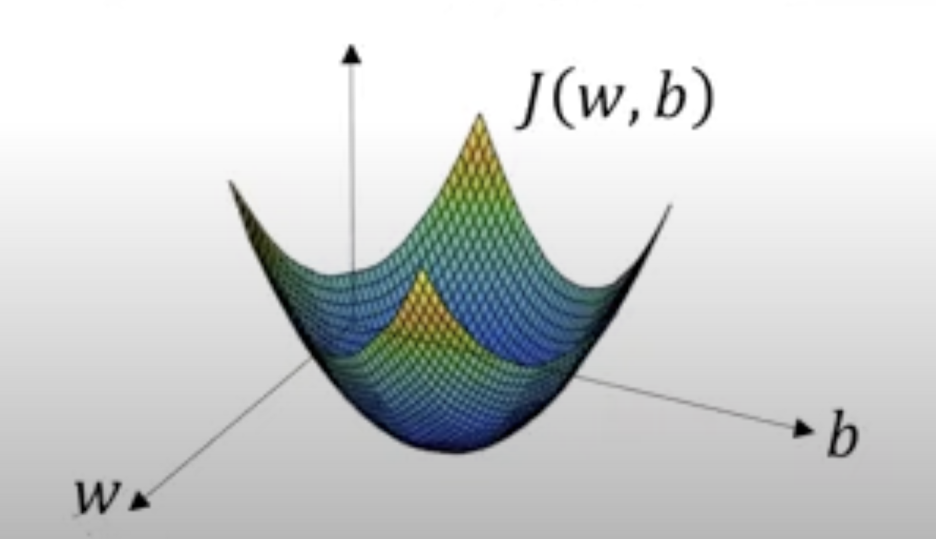
최소가 되는 변수 값을 과정은 똑같습니다.
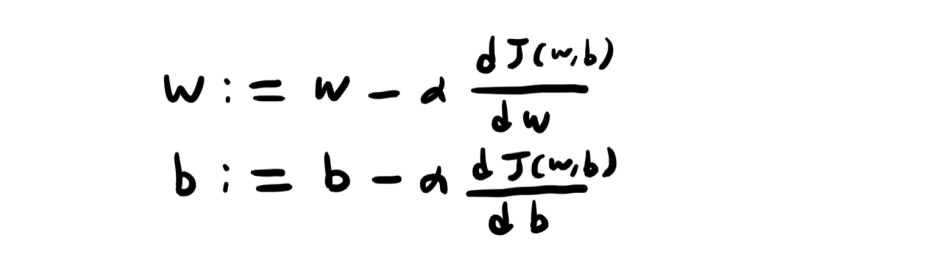
편미분을 할 때에는 d가 아닌 꼬부랑d를 사용한다고 하는데요, 중요 내용이 아니니 넘기겠습니다.
이후 3강 동안 미적분의 기초에 대해 다룹니다. 수2만 공부했어도 모두가 아는 내용이니 넘어가도록 하겠습니다.
2-(7) Computation Graph
Computation Graph
식을 계산할 때의 과정을 쪼개어 마치 그래프처럼 나타낸 것입니다.
Computer Architecture 과목에서 배운 Mips Architecture과 상당히 유사한 느낌이었습니다. 예를 들어J(a,b,c)=3(a+bc)라는 식이 있다면
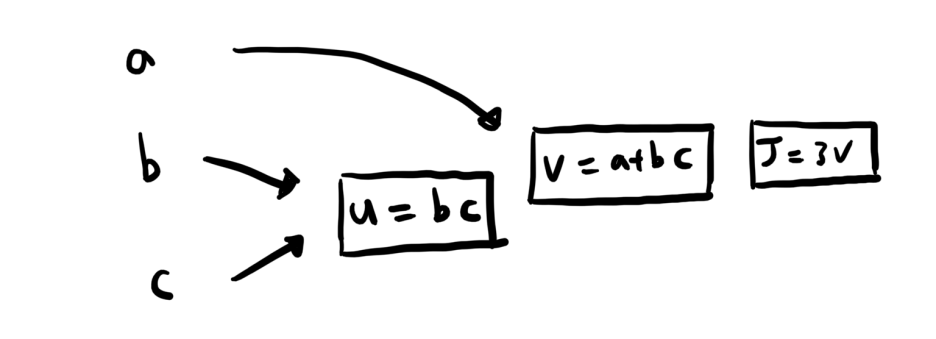
다음과 같은 과정으로 일일이 쪼개주는 것을 의미합니다. 정말 별 게 없습니다.
2-(8) Derivatives With Computation Graphs
에서는 체인룰과 Computation 그래프를 활용한 미분을 배웁니다.

2-(9) Logistic Regression Gradient Descent
로지스틱 회귀(Logistic Regression)에 Computation Graph를 실제로 적용해본다.
한 개의 샘플을 훈련시키는 과정을 배웁니다. 먼저 da,즉 최종 결과값 dL/da를 구해볼까요?
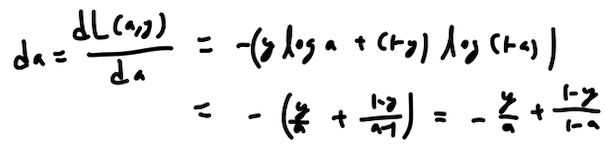
da는 다음 과정을 거쳐 구할 수 있습니다.
dz는 앞에서 언급한 체인룰을 통해서 구하는데요,
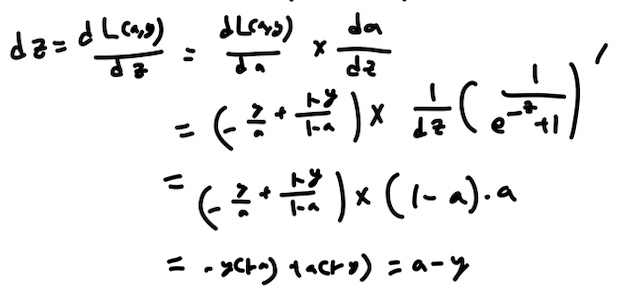
같은 방식으로
dw1,db를 구하면
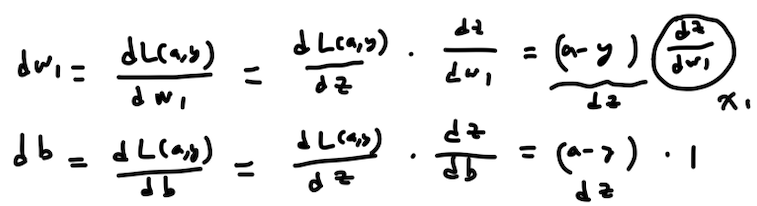
사진 설명을 입력하세요.
이렇게 체인룰을 활용하여 구할 수 있습니다.
이제 w1,w2,b의 값을 업데이트 하는 일만 남았습니다.
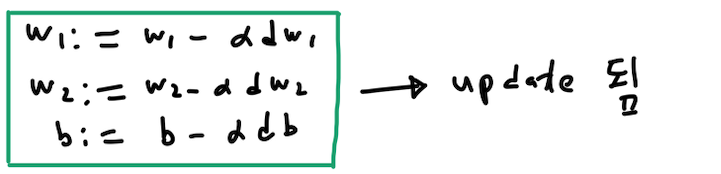
다음과 같이 값을 업데이트 하면 됩니다. 기울기 값을 알아야지 값을 업데이트 할 수 있기에 이러한 작업을 해온 것입니다.
2-(10) Gradient Descent on m Examples
하나가 아닌 m개의 샘플을 사용한다고 해도 달라질게 없습니다. 미분 값의 평균을 구해서 업데이트 하면 그만입니다.

코드는 다음과 같습니다. 2-(9)에서 배운 기울기값 구하는 방법을 똑같이 적용하면 되는데 평균을 구하기 위해서 나누기를 해주는 것입니다.
하지만 하나의 문제점이 생기는데, 이중 for 문을 써야됩니다. 특성이 두 개인 위의 경우에는 상관이 없으나, 특성이 많아지면, 이중 for문은 굉장히 비효율적입니다. 그렇기 때문에 벡터화를 통해 이중 for문을 쓰지 않고 코드를 짜게 됩니다. 4주차에는 벡터화와 파이썬 실습으로 찾아뵙도록 하죠.
'Andrew Ng(Deep Learning)' 카테고리의 다른 글
| 앤드류응 교수님 딥러닝 학습일지 실습-(2) (부제:야옹~난 고양이야!) (1) | 2023.06.05 |
|---|---|
| 앤드류 응 교수님 딥러닝 학습일지 실습(1) (0) | 2023.06.05 |
| 앤드류 응 교수 딥러닝 학습일지-(4) (0) | 2023.06.05 |
| 앤드류 응 교수 딥러닝 학습일지-(2) (0) | 2023.06.05 |
| 앤드류 응 교수 딥러닝 학습일지-(1) (0) | 2023.06.05 |


