본문 바로가기
Linear Algebra

선형대수학 빠르게 요약하기~

탱탱구리뱅뱅 2023. 6. 5. 23:32
반응형

[본 게시글은 고려대학교 COSE111 김승룡 교수님의 전산수학1을 듣고 정리하기 위해 작성한 글입니다.]

전산수학

 

1.1 Systems of Linear Equations

  • Linear equation의 해
    • inconsistent(해가 없다)
    • consistent(해가 있다)
    • uniqueness(유일성)
  • Matrix
    • essential information of a linear system recorded compactly in a rectangular array called matrix
      • set of linear system
    • coefficient matrix
    • augmented matrix
    • size of a matrix
      • m x n ( rows and columns)
  • Elemantary Row Operations
    1. Replacement
    2. Interchange
    3. Scaling
  • Row Equivalent
    • two matrices are called row equivalent if there is a sequence of elemantary row operations that transform one into other.

1.2 Row reduction and Echelon Forms

  • non zero row or column means a row or column that contains at least one nonzero entry

-leading entry of a row refers to the leftmost non zero entry

1.9 연습 문제 보기. 2.1 2.2 2.3 2.5 2.8

1. Echelon matrix is a matrix in echelon form

  • matrix can be row reduced into many echelon forms but there is only one reduced echelon form.
  • If a matrix A is row equivalent to an echeoln matrix U we call U an echelon form of A.

2. Pivot Positions

  • row operations to obtain the reduced echelon form from echelon form do not change the leading entries.
    • leading entries are always in the same positions in any echelon form obtained from a given matrix
  • Row reduction algorithm
    • step 1-4 is called the forward phase(creates a echelon form)
    • step 5 is called a backward phase(creates a reduced echelon form)
  • Basic Variables
    • variables corresponding to pivot columns in the matrix are called basic variables
  • Free Variables
    • variables that are not basic variables
  • example
  • Fundamental questions (Existence and uniqueness)
  • Parametric descriptions of Solution Sets(Example)

1.3 Vector Equations

  • matrix with only one column is called a Vector
  • Rn n means number of rows(as vectors have only one column)
  • Parallelogram Rule for Addition
    • 벡터 덧셈 평행사변형법
  • Linear Combinations
    • y=c1v1+c2v2+c3v3+...cpvp
  • Definition of Span
    • zero vector is in span too.

  • 헷갈릴만한 statement
    • The set Span{u,v} is always visualized as a plane through the origin
      • false (u might be the multiple of v)

1.4 The Matrix Equation Ax=b

  • 헷갈린 만한 부분들
    • Every matrix equation Ax=b corresponds to a vector equation with the same equation set.(True)
    • 1.5 Solution Sets of Linear Systems
  • Homogenous system
    • A system of linear equations is said to be homogenous if it can be written in the form Ax=0
    • if x=0 it is called the trivial solution
    • non zero vector x that satisfies Ax=0 is called a non-trivial solution
    • 만약 모두 basic variable이면 trivial solution 만 존재
  • Parametric vector form

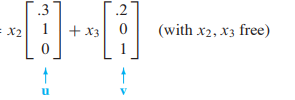
  • x=p+tv
    • tv는 homogeneous equation의 해와 동일.
  • Solutions of Nonhomogeneous Systems

  • 헷갈릴만한 문제들
    • the solution set of Ax=b is the set of all vectors of the form w=p+tv, where tv is any solution of the equation Ax=0
      • 거짓. 해가 없을 수도...
    • The equation Ax=b is homogeneous if the zero vector is the solution
      • YES!!!
    • Ax=b 해가 존재하려면 모든 row에 피봇 포지션
    • Ax=0이 non trivial solution 존재하려면 최소 한개의 free variable (pivot column 아닌게 존재해야됨)

1.7 Linear Indepence

ex)

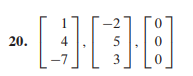
  • linearly dependent

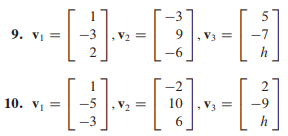
  • span 이랑 linearly dependent 구분하기
  • span은 v1,v2 연산 결과가 v3
  • linear independent 는 v1,v2,v3 연산결과가
  • linearly dependent 라고 해서 모두 다른 벡터의 연산으로 나타낼 수 있는 것은 아님.(c가0인경우)
    • ex)
  • 헷갈릴만한 문제들
    • zero vector 경우가 있기에 거짓.

1.8 Introduction to Linear Transformations

  • domain: Ax=b에서 x
  • codomain: Ax=b에서 b
  • image: the vector T(x) in Rm.
  • range: the set of all image of x
  • linear transformation

1.9 The Matrix of a Linear Transformation

  • A is called the standard matrix for the linear transformation T

  • the columns if the standard matrix for a linear transformation from Rn to Rm are the images of the columns of the nxn matrix.

 

![onto is same with existence question]

onto is same with existence question

  • onto 이면 Rm을 span 해야됨
  • span 하려면 모든 b에 대하여 성립
  • every row에 pivot

one to one is same with the uniqueness question


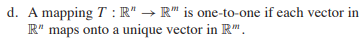
False(모든 b가 x에 의해 결정되는 것이 중요)

증명) p이면 q이다, !p 이면 !q이다 쓰기

  • one to one 이면 independent
  • independent는 dependent 여부 따지기랑 동일
  • free variable 존재하나?

(25-28번)예의주시하기!

2.1 Matrix Operation

  • diagonal entries
  • matrix[i]j
  • Equal matrix
    • size가 같고 모든 칼럼이 동일
  • Matrix Multiplication

2.2 The Inverse of a Matrix

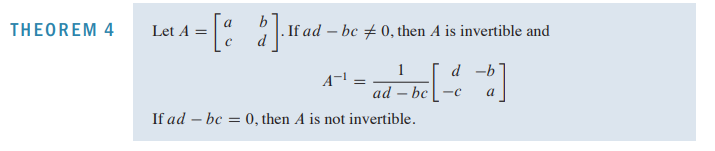
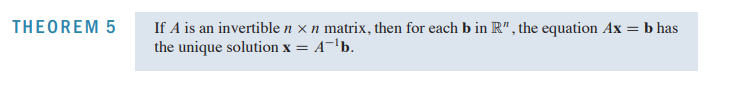
  • Elementary matrix
    • one that is obtained by performing a single elementary operation on an identity matrix
  • Each elementary matrix is invertible

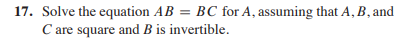
2.3 Characterizations of Invertible Matrices

  • Invertible Linear Transformations

2.5 Matrix Factorizations

  • The LU Factorization

2.8 Subspaces of Rn

  • Definition
  • closed under addition and multiplication
  • zero vector도 subspace
  • zero subspace
  • column space

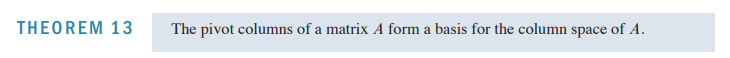
## 2.8 subspaces of Rn

dimension: 하나의 subspace를 이루는 basis의 개수

rank: column space의 basis 개수 (pivot의 개수와 같음)

  • pivot column이 column space의 basis를 결정하기 때문

hint) Nul A는 Ax=0의 해

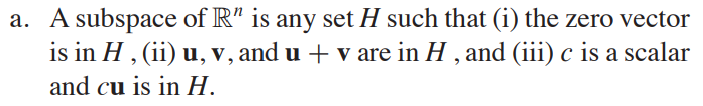
  • 정답 공개c. Null space에서는 변수의 개수만큼의 subspace에 들어가 있음!
  • a.거짓(모든 벡터에 대해 라는 말이 없음)

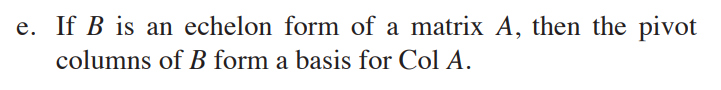
  • 정답 공개
    • dependent 여부는 결정 되지만, 벡터가 변화하기 때문에, Col A가 아닌 Col B의 것이다. (Col A ≠ Col B)
    • 참고

2.9 Dimension and Rank

False

(subspace의 정의:zero vector가 포함 되어야 함)

6.1 Inner product, length, orthogonality

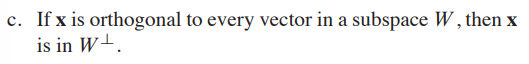
  • 정답
  • 둘 다 true!!

거짓!!c가 0일 수도 있답니다!

6.2 Orthogonal sets

증명 c1v1+c2v2….cnvn=0 에다가 v1내적하기!

모든 orthogonal set가 linearly independent 한 것은 아님!(zero vector 때문!!)

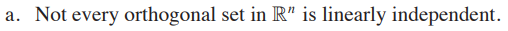
  • 정답 공개
  • 거짓{0,0,0,0,0}도 orthogonal 하다. 그런데 linearly dependent 함

6.3 Orthogonal Projections

6.4 The GRAM-SCHMIDT PROCESS

v1,v2,v3가 zero vector일수도 있음

6.5 LEAST-SQUARES PROBLEMS


사고의 순서: b→c→a 순서!

Ax=0이 해가 trivial 함

A^tA 해가 independent 함!

invertible 하니까 해가 유일!

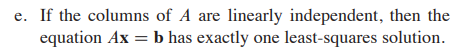
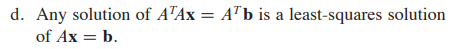
정의 읽기!

이 문제정말정말 중요!!!

//closest to b는 b(hat)…근이 아니다!

A가 invertible 해야지 성립함!

5.1 EIGENVECTORS AND EIGENVALUES


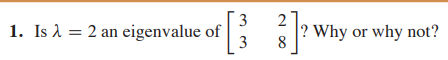
non zero vector 말고도 해를 가지느냐?

dependent 한 지를 따져야함!.

free variable이 하나라도 있어야됨!

Ax=λx를 만족하는 λ를 eigenvalue라함 non trivial solution을 의미하기에 x는 non zero 이어야 하지만, 저 식을 만족하기만 하면 되기에 λ는 0이어도 상관이 없음.

Ax=λx에서 λ가 0이고 eigen value 이면 non triavial 솔루션이 존재하고, Ax=0 의 해가 유일하지 않으므로, dependent, not invertible 함!

5.3 Diagonalization

7.1 Symmetric Matrix

A transpose는 A 이므로 A는 symmetric함!symmetric 해야 orthogonally diagonalize 할 수 있음!

  • symmetric 한지 체크부터 하기 (orthogonally diagonalize 하기 전에!)
  1. diagonalization( decomposing eigen value)
    • 첫번째 단계에서는 eigen value 를 구하는 게 최우선임
    • 다른 eigen value 라면 서로 orthogonal 하지만, 같은 eigen value 아래에서는 그렇지 않으므로, 그램 슈미트 를 써준다.
    • orthogonal matrix는 orthonormal sets들로 이루어져 있으므로, generalize를 해줘야 한다!.
    • Symmetric Matrix의 특징들
  2. b. characteristic equation에서 특정 eigenvalue의 거듭제곱 수 만큼의 basis가 형성됨 (dimension).
반응형

티스토리툴바